ドリッパーから水が落ちる時間を計算してみた

〜トリチェリの法則で排出時間を可視化してみた〜

---

はじめに｜なぜ排出時間を計算してみたか

コーヒーの抽出において、ドリッパー内に滞留している時間は重要な要素ですが、体感や経験則ベースで「だいたい〇秒で落ちる」とされている部分を、数値化してみたいと思っていました。

• タンク形状
• 注ぎ口のサイズ
• 重力

こういった条件が、実際に水が落ちる時間にどう影響するのか。

そこで今回は、トリチェリの法則を使って、円台タンクの排出時間を計算してみました。

＊ペーパーフィルターも無しの条件なので実用性は乏しいと思いますがまずは簡単なところからやってみました。

---

ドリッパーの形と基本式

とりあえず手始めに計算しやすい形状のハリオV60から（02サイズ）。

ネット情報などから見積もって寸法は下記のように設定しました：

• 底半径 $r_1 = 10\ \mathrm{mm}$
• 上半径 $r_2 = 58\ \mathrm{mm}$
• 高さ $H = 83\ \mathrm{mm}$

高さHは、底半径（=排出孔径）と上半径と角度(60°)から算出しました。

高さ $h$ のときのタンク半径は、線形補間で表せます：$$r(h) = r_1 + (r_2 – r_1)\frac{h}{H}$$断面積はそのまま、$$A(h) = \pi r(h)^2$$で計算できます。

---

トリチェリの法則で排出速度を計算

小さな穴から水が出る速度は、トリチェリの法則に従います：$$Q = A_o \sqrt{2 g h},\quad A_o = \frac{\pi d_o^2}{4},\ d_o = 20\ \mathrm{mm}$$これをタンク断面積にあわせて整理すると、$$\frac{dh}{dt} = \frac{A_o}{A(h)} \sqrt{2 g h}$$という微分方程式になります。

---

排出時間の計算

タンクを ほぼ空にするまでの時間 $T$ は、$$T = \int_{h_\mathrm{cut}}^{h_0} \frac{A(h)}{A_o \sqrt{2 g h}} dh$$で求められます。

ここで $h_0 = H = 83\ \mathrm{mm}$、カットオフ水位 は今回は0とします。

---

半径を代入して解析積分

半径の二次式展開すると、$$r(h)^2 = r_1^2 + 2 r_1 (r_2-r_1)\frac{h}{H} + (r_2-r_1)^2 \frac{h^2}{H^2}$$となります。

これを積分に代入すると、閉じた形の解析式で排出時間を求められます。

$$T = \frac{2 \pi}{A_o \sqrt{2 g}} \Big[ a h^{1/2} + \frac{2}{3} b h^{3/2} + \frac{2}{5} c h^{5/2} \Big]_{h_\mathrm{cut}}^{h_0}$$ここで$$a = r_1^2, \quad b = \frac{2 r_1 (r_2-r_1)}{H}, \quad c = \frac{(r_2-r_1)^2}{H^2}$$です。

---

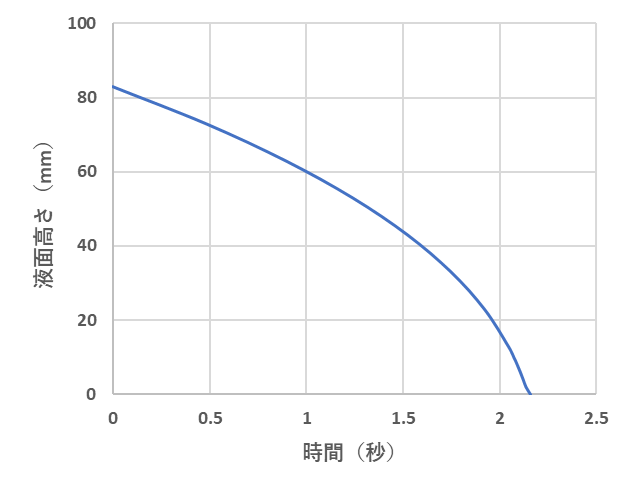
計算結果と今後の展望

• この条件で計算すると、落ちきるまでに約2.16秒かかることが分かりました。
• サイズが違ったら？、穴の大きさや数が違ったら？、など色々と気になることはあると思うのでまた前提を変えた計算もやってみようと思います。

---

まとめ｜数式で見る流体の滴下現象

今回の計算を通じて、次のことが分かりました：

1. トリチェリの法則＋ドリッパー形状を考慮すれば、排出時間を厳密に求められる
2. ドリッパーの形状（底と上の比率）が、排出時間に直結する
3. 実際の観測では、穴の大きさや重力だけでなく、摩擦や水面の乱れも影響する可能性があるのでこのあたりの精査は今後の課題

次回は、孔径の違いや数の違い、の影響を求めてみたいと思います。

最終的にはフィルターの影響、豆の影響（さらに粒径を変数としてどうなるか）を考慮して初めて意味のあるものになるとは思いますが・・・。

それではまた！